湿地斑块与生态要素组成。建筑尤其是居住建筑多为具有中庭或庭院的内聚型建筑，可以明确内部的核心公共空间。这种分子型的空间结构清晰明确，有利于功能区间的组织。

    校园中以景观绿化为核心的分子型组团结构与村落中以多要素组合的公共空间为核心的组团结构相似，这是两种网络结构能够相互融合的基础。

（三）研究内容和方法

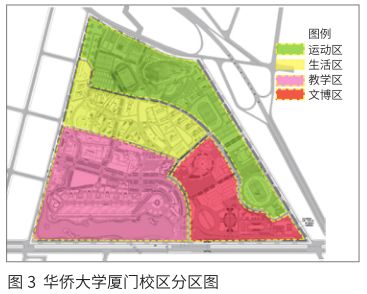
    华侨大学厦门校区分为教学区、生活区、文博区和运动区4个分区，目前教学区、生活区基本建设完成，运动区部分建设完成，文博区尚未开始建设(图3)。本文研究的重点是如何在总体层面和单体层面，将原规划中文博区所设定的校园功能创造性地融入现有村落社会和空间结构中。区别于一般的基于功能分区的校园规划，本项目采用算法设计的方法进行规划(表1)。

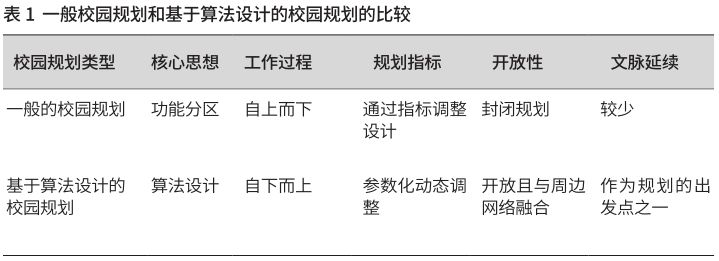
    所谓算法设计，即使用数字化编程(Scripting)技术解决设计问题。算法设计强调理由和逻辑过程的准确性与可控性，更强调自下而上的工作过程，而非形式结果。研究通过探索校园与村落内在的构成及演化规律，提出校园与村落空间模式的相似特征，并基于相似特征选择合理的算法将两者的关键要素整合到统一的网络中，在保证校园与村落各自独立运作的同时，使两者发生相互间的空间共享与资源交换。

二  算法介绍与规划思路

（一）算法介绍

    Circle Packing 算法 ( 圆形堆叠算法)、Voronoi算法(泰森多边形算法)和Delaunay算法(三角剖分算法)等算法的几何原型都属于分形系统，具备分形系统的基本特征，且算法之间也具有一定的联系。分形系统的基本原则是总体与局部的自我相似和迭代。在抽象的分形系统中，没有总体和局部的区别，因为总体和局部的形成都遵循同一种原则。该系统空间中的点不是零散的个体，各个点之间具有平滑的过渡。堆叠(Packing)，即空间堆叠，指的是依据一定的规则，在有限的空间范围内尽可能多地放置限定大小和形状的单元体，以避免空间浪费，可应用这种方式构建分形系统。

(1)Circle Packing算法。

    在几何学中，Circle Packing算法是指用相同或不同半径的圆形相切并且无重叠地填充限定的区域范围，要求每个圆至少有两个圆与之相切。Circle Packing图案的要素包括圆的个数、各圆心位置、圆的半径、相切关系、边界形态与尺寸。

    Circle Packing算法的生成可遵循多种逻辑，研究主要借助Grasshopper程序和Kangroo插件，模拟圆形物体在力的作用下向某一核心聚拢的物理过程，空间的中心对所有的圆形中心产生吸引力，使得随机分布的圆形向中心靠拢，不同的圆形中心彼此会产生斥力，斥力作用范围等同于圆的半径。在中心引力和相互斥力的作用下，经过一段时间的运动，所有的圆会趋向于一种动态平衡，形成特定的图案。

在设计中，Circle Packing算法可用来解决大量设计对象在场地中的分布问题。

(2)Voronoi算法与Delaunay算法。

    Voronoi算法是指在平面中随机分布的点集按照对偶原则，将平面划分为多边形团。对偶原则，即在Voronoi图中每一条线都是相邻两个点之间线段的垂直平分线。由随机点两两连线所得的三角形图即为该 Voronoi 图的对偶图形，又称德劳内(Delaunay)三角形。在三维空间中，若任意点划分的相临多面体均满足对偶原则，则该多面体团亦为Voronoi结构，其空间控制点具有与平面Voronoi图控制点相同的特性。

    Voronoi图的要素包括凸多边形重心( 控制点 )、凸多边形边界、边界垂直平分线(连接重心)和凸多边形区域。凸多边形区域 Voronoi 图中任意一个凸多边形(泰森多边形)仅含有一个控制点；泰森多边形内的任意点到相应控制点的直线距离最近；位于泰森多边形边上的点到其两边的控制点的直线距离相等。泰森多边形镶嵌可以在重复单元性的基础上不留缝隙镶嵌，每个单元具有明确的中心但没有固定的边界形态，多边形构成的网络形态具有分形性和有机性。

    在设计领域，Voronoi算法主要运用于空间定性分析、空间系统组织、空间形态分割和最优路径选择等方面。

（二）规划思路